从二叉树到红黑树
还记得二叉树么, 今天将复习二叉树、二叉查找树、平衡二叉查找树、红黑树、递归树
二叉树
关于书的定义,我就不赘述了,也记不住。如图所示,需要了解父节点、子节点、根节点、叶子节点。
高度、深度、层:

上面的概念需要理解:节点的高度从叶子节点开始算;深度从跟节点开始算。
树中最常见的是二叉树,满二叉树可以理解;完全二叉树如上图所示,定义为叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。
之所以给他们取名字,因为完全二叉树相对于其他“缺胳膊少腿”的树在顺序存储中是不同的。
表示(存储)二叉树
顺序存储法。基于数组的顺序存储法,将根节点存储在下标i=1的位置,其左节点存储在下标2*i=2的位置,右节点存储在2*i+1=3的位置,以此类推。反过来,子节点下标为m时,他的父节点下标为m/2。换句话说,顺序存储法存储二叉树到数组中,在数组中表现的就是按层遍历该二叉树。
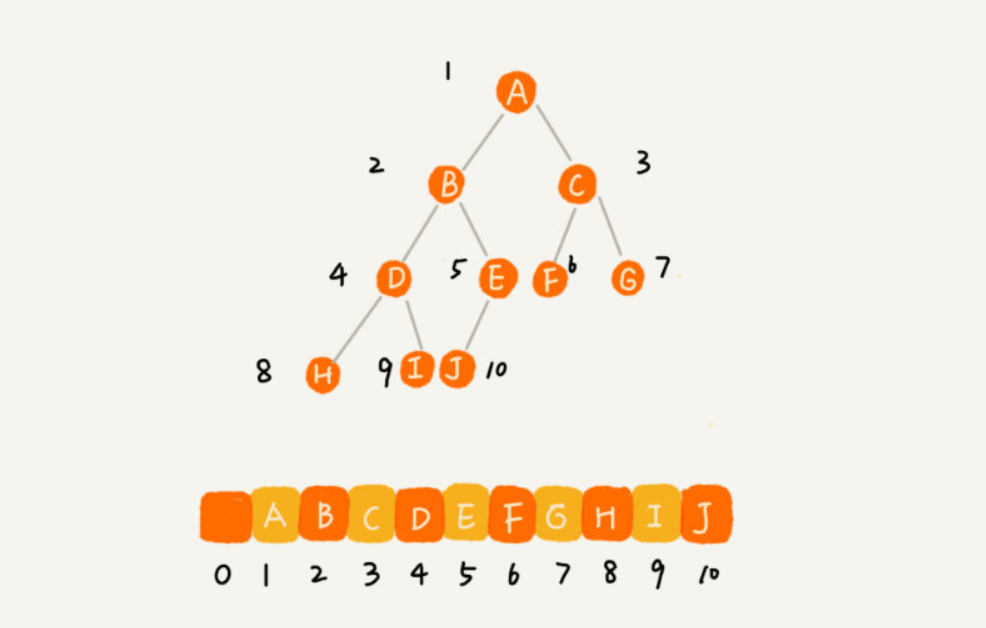
到这里可以发现,引入完全二叉树就是为了适应在数组中存储二叉树这种做法——刚刚好将数组存满了。如果不是完全二叉树,那么数组中一定会出现空缺的情况。
链式存储法。该方法使数据的组织更像二叉树,一个结点包含左右子节点的指针+数据。
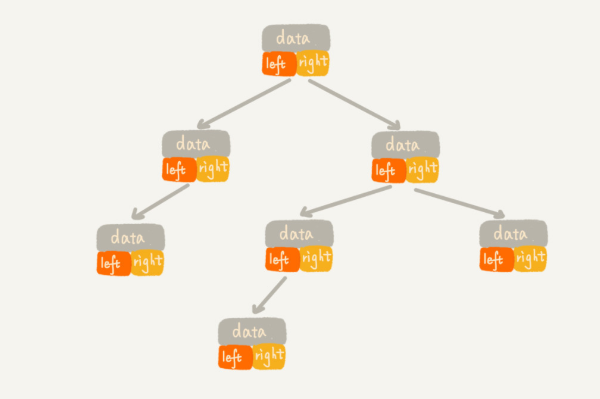
遍历二叉树
有若干种方法遍历二叉树的所有结点:
前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
记得考试时比较爱考这个,我想前、中、后序遍历,是相对于父节点来说的,记住这个就好。
对二叉树的遍历过程是递归的,递推式如下:
1 | |
学习一下代码:
1 | |
如果你与我一样不太能理解,写完上面的代码后会对他的遍历有更深刻的认识!遍历的复杂度为O(n)
层次遍历。使用队列实现。
二叉查找树
Binary search tree最大的特点是支持动态数据集合的快速插入、删除、查找。
尽管散列表也高效,二叉树亦有过人之处:
- 散列表中数据无序存储,对二叉查找树仅需中序遍历;
- 散列表扩容耗时,遇到散列冲突时不稳定;二叉查找树相对二叉树性能稳定了,约为O(logn);
- 理论上散列表查找效率高,但可能存在的hash冲突使得复杂度提高,所以实际查找速度不见得比BST高;
- 散列表构造复杂,需要考虑散列函数设计、冲突解决,扩容缩容。平衡二叉树只需考虑平衡问题。
- 散列表为避免过多散列冲突,装载因子不能太大,存在存储空间浪费。
好,那二叉查找(搜索)树,到底是啥呢?
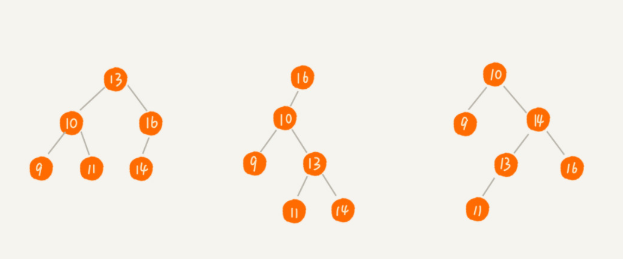
BST的设计是为了实现快速查找,为此要求书中任意一节点的左子树小于它,右子树大于(等于)它的值。这里的等于是在处理插入相同值时特殊设计的一种方式,还有其他方法,我在后面介绍。
BST 的查找操作
1 | |
BST的插入操作
一般插在叶子节点上,将插入值与节点上的做比较即可。

1 | |
上面的代码其实是缺少对重复数据的处理的,
对有重复的二叉查找树,插入:
- 将重复的数据放该结点的右子树的最左子节点;
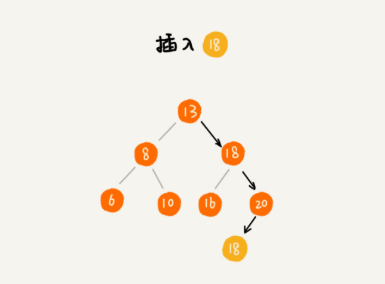
- 数据的组织结构更改,存储链表指针指向值相同的数据;
对有重复数据的二叉查找树,查找:
- 遇值相同的节点后,继续查找右子树,直到遇到叶子节点;

对有重复数据的二叉查找树,删除:
- 先找到每个要删除的节点
- 删除操作(调整树)
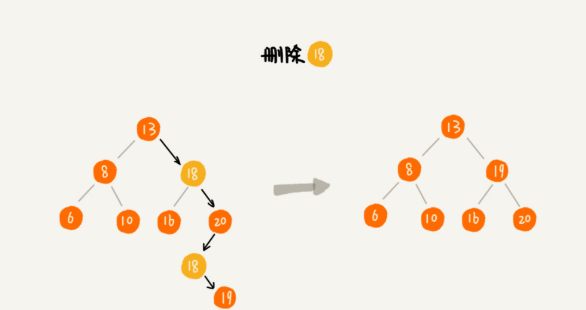
BST的删除操作
删除操作相对复杂,需要考虑不同情况:
- 要删除的节点无子节点
- 要删除的节点只有一个子节点;
- 要删除的节点有2个子节点:找右子树中最小的节点替换上
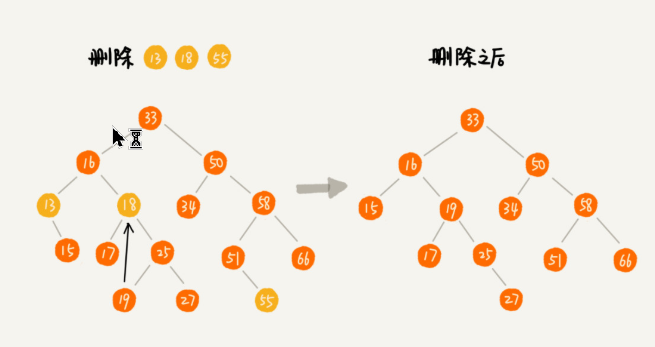
1 | |
删除操作代码有点迷,!!!!
查找最大(小)节点
查找前驱、后继节点
中序遍历二叉查找树
二叉查找树的复杂度与树的高度有关,即O(logn)
25红黑树
作者讲到许多工程中更喜欢使用红黑树,这是因为普通书在动态更新后会导致复杂度退化。而RBT对动态插入、删除、查找比较友好。
其中RBT不像AVI树那样必须要求左右子树高度差在1内,允许一定的高度差;他的左右螺旋也是需要理解的,我在温习时细节已经记得不是很清楚了。这里就不赘述了。
28 堆与堆排序
在若干排序中,堆排序的实际排序是没有快排快的,这是为什么呢?
堆排序是堆的一种应用,它是原地排序算法,O(nlogn)。
什么是堆:当我看到大顶堆、小顶堆时,立刻回忆起堆的大体样貌,一种特殊的树。
堆:
是一棵完全二叉树;每个节点都大于等于 或 小于等于他的子节点。
完全二叉树可以存储在数组中!
