王铮老师《算法》系列文章之30-36。
提纲:本节我需要复习图、深度和广度优先搜索、字符串匹配、Tire树、AC自动机。
图的表示
无向图:如微信的人际关系;
有向图:如微博,关注是相互的;
带权图:qq好友间亲密度;
邻阶矩阵存储 adjacency 依赖于二维数组,顶点之间对应关系为0或1或权重。
稀疏图:浪费空间。
好处:方便计算,可将图的运算转换为矩阵之间的运算。如求解最短路径:Floyd-Warshall算法
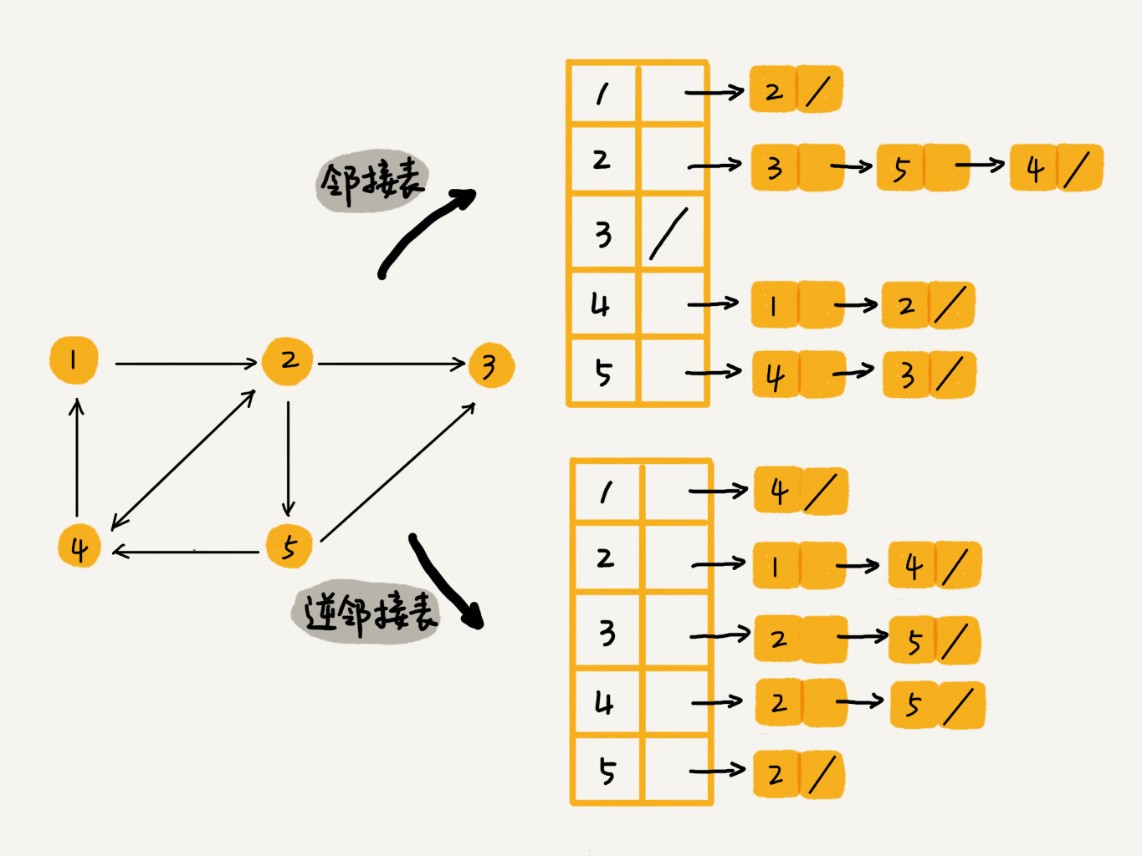
邻接表存储方法 Adjacency List图片介绍
可以将邻接表中的链表改成红黑树等树,以提高效率。
当我们需要查找用户的粉丝列表(该用户被哪些人关注了),在使用邻接表存储时存在问题,需要使用逆邻接表,也就是每个顶点的链表中存储指向这个顶点的顶点。
因为,像较于复杂的红黑树,跳表空间复杂度为O(n),时间复杂度为O(logn),并且是有序存储数据,适合分页读取。
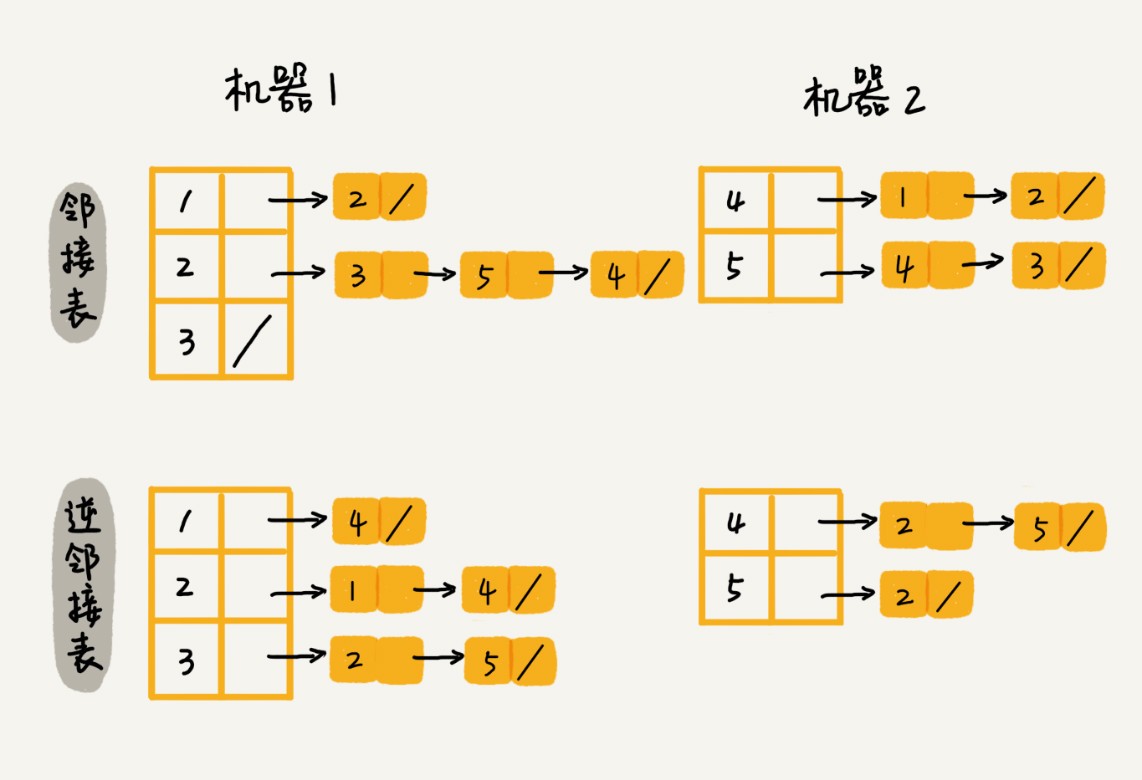
需使用Hash算法(数据加密、唯一标识、数据检验、散列函数、负载均衡、数据分片、分布式存储)将数据分片,将邻接表存储在不同机器上。这样在查询顶点关系时,使用相同的hash算法定位所在机器,再在机器上查找。
数据库存储法 小结 了解了图,二维数组存储方式和链表存储方式,但是对大规模数据,如微博拥有几亿用户数据,需要将数据分片。为了便于查找,可将链表换为高效的平衡二叉查找树、跳表、散列表。
其实,图的使用还有:知识图谱、地图、微信中的无向图。
深度和广度优先搜索 社交中有“可能认识的人”这一功能,即通过用户之间的N度连接关系来找到。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public class Graph { private int v;private LinkedList<Integer> adj; public Graph (int v) {this .v = v;new LinkedList [v];for (int i=0 ; i<v; ++i){new LinkedList <>();public void addEdge (int s,int t) {
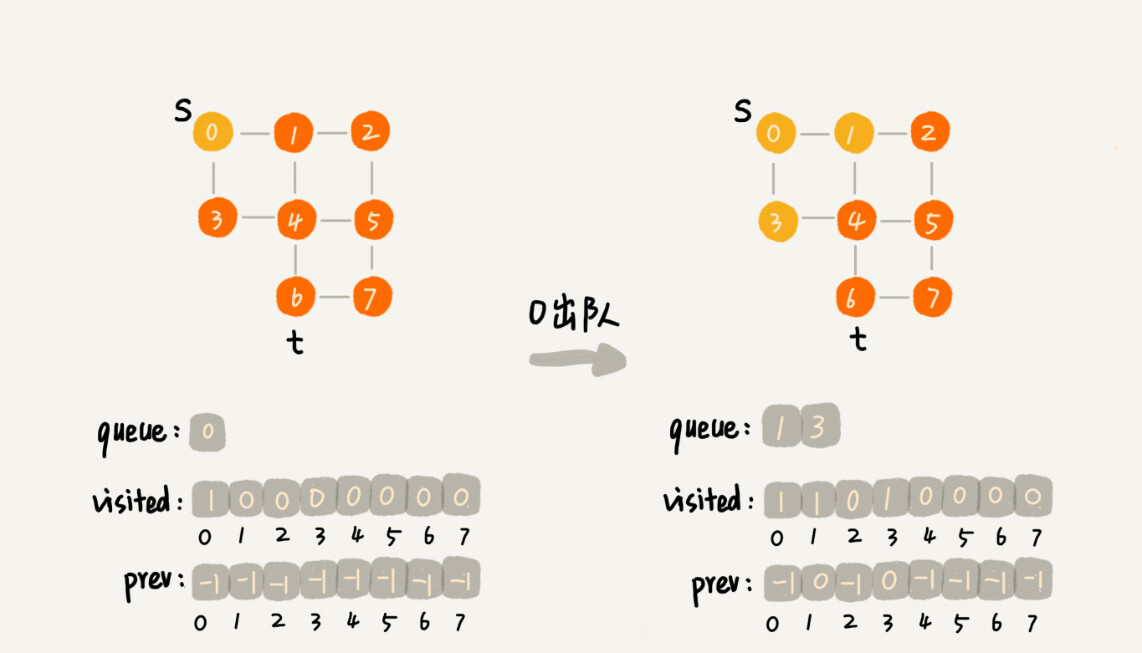
广度优先搜索 Breadth First Search 一种地毯式、层层推进的搜索策略。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 public void bfs (int s, int t) {if (s==t) return ;boolean [] visited = new boolean [v];true ;new LinkedList <>();int [] prev = new int [v];for (int i=0 ; i<v; ++i){1 ;while (queue.size() != 0 ){int w = queue.poll();for (int i=0 ; i<adj[w].size(); ++i){int q = adj[w].get(i);if (!visited[q]){if (q ==t){return ;true ;private void print (int [] prev, int s, int t) {if (prev[t] != -1 && t !=s){" " );
深度优先搜索(回溯思想) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 boolean found = false ; public void dfs (int s, int t) {false ;boolean [] visited = new boolean [v];int [] prev = new int [v]; for (int i=0 ; i<v; ++i){1 ;private void recurDfs (int w, int t, boolean [] visited, int [] prev) {if (found==true ) return ;true ;if (w == t){ true ;return ;for (int i=0 ; i<adj[w].size(); ++i){int q = adj[w].get(i);if (!visited[q]){
来看看复杂度,在遍历的时候,每个顶点要进出一遍队列,每个边也会被访问一次,其时间复杂度就是$O(V+E)$ ,在书树中,边的个数E = 顶点个数V - 1。
字符串匹配:借助hash BF算法 brute force暴力匹配
模式串一步步在主串中匹配。
RK算法 改进:通过hash算法计算主串中n-m+1个子串的hash值,后与模式串中的hash值比大小…
改进2:计算hash值时需要遍历整个主串。使用K进制数来表示一个子串。
比如要处理的字符串只包含 a~z 这 26 个小写字母,那我们就用二十六进制来表示一个字符串。
将az映射到025这26个数字。
这样每个位的hash值计算独立,每次运算左右移动,加减值即可?
“657” = 6 * 10 * 10 + 5* 10 + 7 * 1
“cba” = “c”*26 * 26 + “b” * 26 + “a” * 1
= 2 * 26 * 26 +1 * 26 + 0 * 1 =
字符串匹配:文本编辑器的查找功能 BM算法 全称为Boyer-Moore算法
这些算法都是在寻找一种规律:遇到不匹配的字符时,将模式串往后多滑动几位。
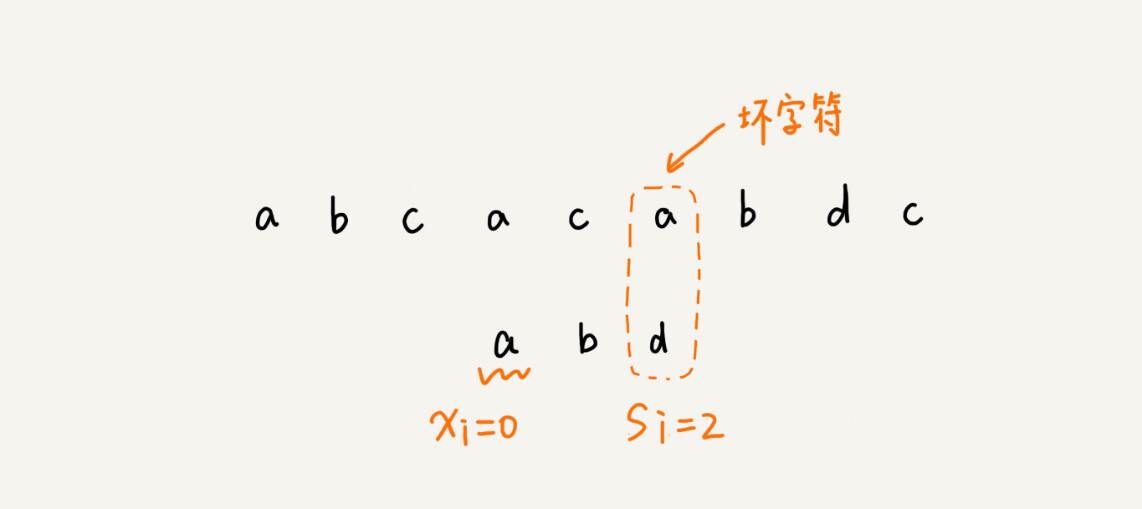
1.坏字符规则 bad character rule 按照模式串下标,倒着匹配。
原理:当发生不匹配时,把坏字符对应的模式串中的字符下标记为si,若坏字符在模式串中存在,将最靠后 的字符下标记为xi。如模式串中不存在坏字符,xi=-1.那么模式串往后移动si-xi。如图
不过,单纯使用坏字符规则还是不够的。因为根据 si-xi 计算出来的移动位数,有可能是负数,比如主串是 aaaaaaaaaaaaaaaa,模式串是 baaa。不但不会向后滑动模式串,还有可能倒退。所以,BM 算法还需要用到“好后缀规则”。
主串aaaa 模式串baaa 匹配到第一个字符时,坏字符为a此时,si=0 xi=3此时会出现负数。
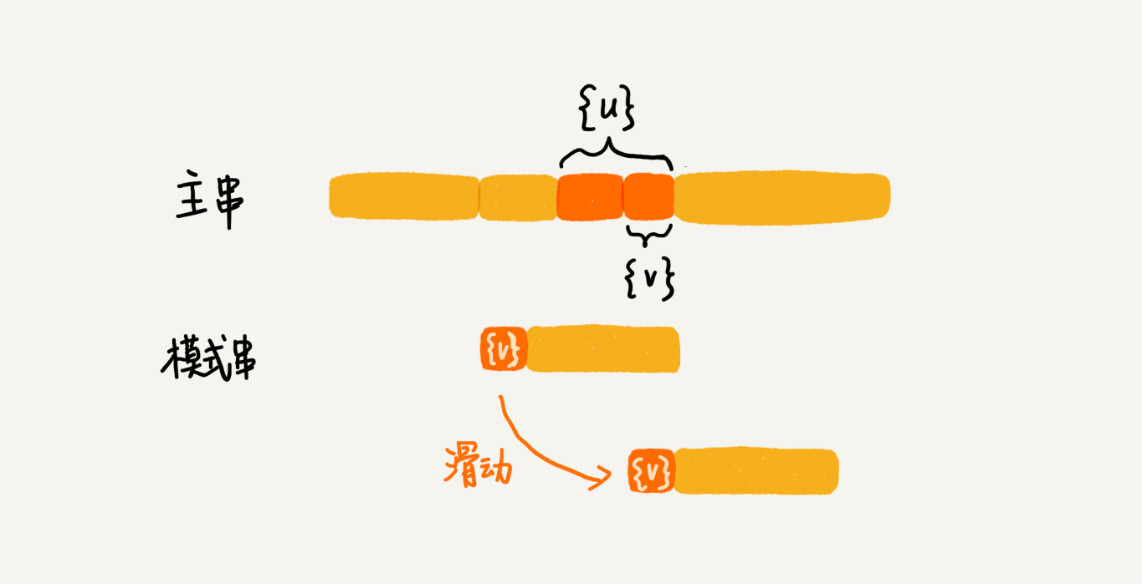
2.好后缀规则
好后缀,记为{u},模式串与主串已经匹配的后缀部分。
将{u}在模式串中再匹配查找,若找到了就将模式串滑动到与子串、主串对齐的位置。
若在模式串中找不到相等的{u}子串,再将{u}的后缀子串中 找到最长的且可与模式串的前缀子串匹配的子串{V}。
换句话说,需要满足:
1、好后缀在模式串中存在另一个匹配的子串,则移动到最靠后面的子串位置。
2、好后缀的子串中,有与模式串中子串相匹配的情况,需要移动到此位置。
我们可以分别计算好后缀和坏字符往后滑动的位数,然后取两个数中最大的,作为模式串往后滑动的位数 。这种处理方法还可以避免我们前面提到的,根据坏字符规则,计算得到的往后滑动的位数,有可能是负数的情况。
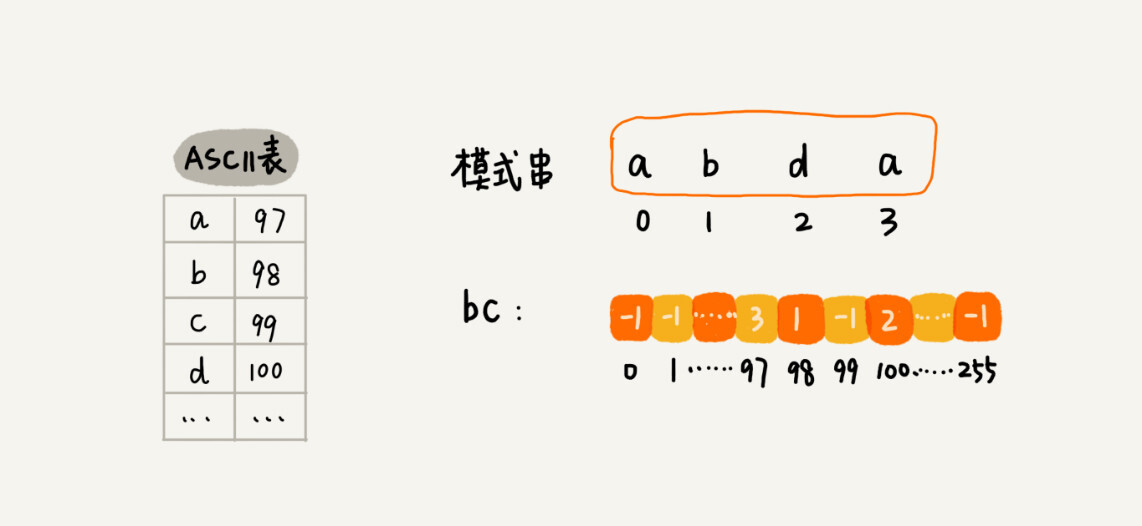
BM算法 代码
数组的下标对应字符串的ASCII码值,数组中存储这个字符在模式串中出现的位置:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public int bm (char [] a, int n, char [] b, int m) {int [] bc = new int [SIZE]; int i = 0 ; while (i <= n - m) {int j;for (j = m - 1 ; j >= 0 ; --j) { if (a[i+j] != b[j]) break ; if (j < 0 ) {return i; int )a[i+j]]); return -1 ;
到这里关于后缀子串的设计我就晕了!!回头再来。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 public class BoyerMooreTest {public static void main (String[] args) {String str = "BBACDEACDBABEACDBACB" ;String pattern = "EACDBAC" ;int index = boyerMoore(str, pattern);"首次出现位置:" + index);private static int findCharacter (String pattern, char badCharacter, int index) {for (int i=index-1 ; i>=0 ; i--){if (pattern.charAt(i) == badCharacter){return i;return -1 ;public static int boyerMoore (String str, String pattern) {int strLength = str.length();int patternLength = pattern.length();int start = 0 ;while (start <= strLength - patternLength){int i;for (i = patternLength-1 ; i>=0 ; i--){if (str.charAt(start+i) != pattern.charAt(i)) break ;if (i<0 ){return start;int charIndex = findCharacter(pattern, str.charAt(start +i), i);int bcOffset = charIndex >= 0 ? i-charIndex: i+1 ;return -1 ;
小结
当需要查找,减少时间复杂度时,可以想到散列表。
当表达式计算开销大,又需要频繁使用,可以考虑预处理与缓存。这就是一个优化过程。
BM特点是 从字符串的最右侧开始匹配、坏字符匹配
字符串匹配:借助BM算法理解KMP算法 KMP算法依然可以寻找一种规律:在模式串与主串匹配过程中,当遇到坏字符后,对已经对比过的好前缀,找到规律,将模式串一次性滑动多位。
也就是,对比得到最长的 主串的好前缀的后缀子串 与 模式串的好前缀的前缀子串,他们是相同的。
即,好前缀的 最长可匹配后缀子串 VS. 最长可匹配前缀子串。
—> 即模式串本身 就可以求解。
next数组(部分匹配值表) 这里,作者使用“一种类似动态规划的方法,按照下标 i 从小到大,依次计算 next[i],并且 next[i]的计算通过前面已经计算出来的 next[0],next[1],……,next[i-1]来推导。 ”
创建next数组,就是要预处理好模式串的匹配情况。这里的运算过程有点绕,可以参考
略..
这里以为参考,他以子字符串”ACDBACDE”为例手算结果:
1 2 3 4 5 6 7 8 "A" 的前缀和后缀都为空集,没有共有元素,共有元素的长度为0 ;"AC" 的前缀为[A ],后缀为[C ],没有共有元素,共有元素的长度为0 ;"ACD" 的前缀为[A , AC ],后缀为[CD , D ],没有共有元素,共有元素的长度为0 ;"ACDB" 的前缀为[A , AC , ACD ],后缀为[CDB , BD , D ],没有共有元素,共有元素的长度为0 ;"ACDBA" 的前缀为[A , AC , ACD , ACDB ],后缀为[CDBA , DBA , BA , A ],最长共有元素为"A" ,共有元素的长度为1 ;"ACDBAC" 的前缀为[A , AC , ACD , ACDB , ACDBA ],后缀为[CDBAC , DBAC , BAC , AC , C ],最长共有元素为"AC" ,最长共有元素长度为2 ;"ACDBACD" 的前缀为[A , AC , ACD , ACDB , ACDBA , ACDBAC ],后缀为[CDBACD , DBACD , BACD , ACD , CD , D ],最长共有元素为"ACD" ,最长共有元素长度为3 ;"ACDBACDE" 的前缀为[A , AC , ACD , ACDB , ACDBA , ACDBAC , ACDBAC ],后缀为[CDBACDE , DBACDE , BACDE , ACDE , CDE , DE , E ],没有共有元素,共有元素的长度为0 ;
计算得到next数组:
子字符串
A
C
D
B
A
C
D
E
对应部分匹配值
0
0
0
0
1
2
3
0
如下图所示,已匹配的字符数为7,已匹配的字符串为ACDBACD,它对应的部分匹配值为3,所以移动位数为7-3=4,所以子字符串向右移动四个字符串:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public static void makeNext (char str[], int next[]) {int len = str.length;0 ] = 0 ; int k = 0 ; for (int i=1 ; i<len; i++){while (k>0 && str[i] != str[k])1 ];if (str[i] == str[k])
KMP算法框架代码 KMP算法需要注意;
计算部分匹配表(next数组)
用位移公式计算,模式串中没有匹配的字符串 就由next数组的位移值向前移动。
动态规划法 生成next数组。
Trie树 又称为前缀树、字典树,专门用于字符串匹配的数据结构,用于在一组字符串集合中快速查找某个字符串的问题。
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
操作1:将字符串集合(一个个字符串插入)构造成Trie树。
操作2:在Trie树中查询一个字符串。
存储:
每个节点 是一个下标与字符映射的数组;
换成有序数组、跳表、散列表、红黑树…,以节省内存(增加了编码难度)
针对一组字符串中查找字符串问题(精确查找),倾向于使用散列表or红黑树。
Trie树适合 查找前缀匹配的字符串。如搜索引擎中的提示功能。
自动补全功能。
1 2 3 4 5 6 // 这里 作者提出了一些思考
AC自动机 Aho-Corasick算法,一种多模式串匹配算法:用多模式串匹配实现敏感词过滤。
目标是:扫描一遍主串,就能查找多个模式串是否存在。
类似于串匹配算法与KMP算法关系,Trie树与AC自动机之间,对多模串额Trie树进行改进,在树上构建了next数组。
AC自动机的构建:
将多个模式串构建为Trie树
在Trie树上构建失败指针(相当于KMP中的失效函数 next数组)
1 2 3 4 5 6 7 8 9 10 11 public class AcNode {public char data;public AcNode[] children = new AcNode [26 ]; public boolean isEndingChar = false ; public int length = -1 ; public AcNode fail; public AcNode (char data) {this .data = data;
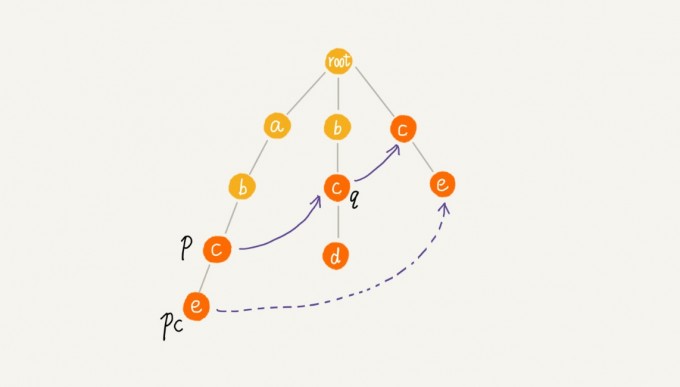
在Trie树上 构建失败指针 AC自动机当中p节点的失败指针指向那个最长匹配后缀子串对应的模式串的前缀的最后一个结点.
我们可以像 KMP 算法那样,当我们要求某个节点的失败指针的时候,我们通过已经求得的、深度更小的那些节点的失败指针来推导。也就是说,我们可以逐层依次来求解每个节点的失败指针。所以,失败指针的构建过程,是一个按层遍历树的过程。
https://static001.geekbang.org/resource/image/51/3c/5150d176502dda4adfc63e9b2915b23c.jpg
在AC自动机上匹配主串 Reference